JKフリップフロップを3分で覚えられる簡単な覚え方を紹介!
皆さんこんにちは。
この記事では、JKフリップフロップの真理値表を簡単に覚える方法を紹介していきます。
情報技術検定の対策をしている工業生の方などに役に立つかと思われますので、参考にしてください。
JKフリップフロップ回路の真理値表
まず、以下の真理値表を見ていだたきたいのですが、この記事にたどり着いた方ならこの表は、おそらくすでに知っていると思います。
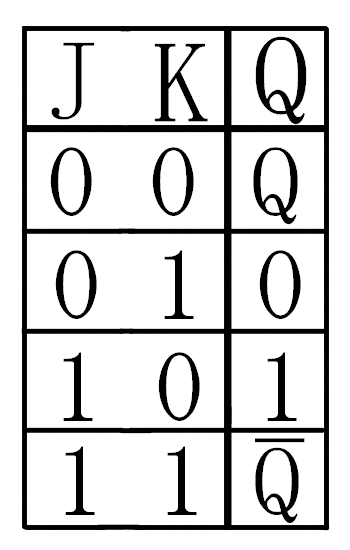
この表は、JKフリップフロップの真理値を表した表になります。
例えば、Jに0、Kに1が入力されたら、出力される値(Qの値)は0になるといった具合です。
表の中に、出力がQやQバーとなっているものがありますが、これは、Qのとき前の値を出力し、Qバーのとき前の値を反転した値を出力するという意味になります。
たとえば前回のQの値が1の時、出力がQだったらそのまま1が出力され、出力がQバーだったら0が出力されるということです。
ちょっとわかりづらいと思ったかもしれませんが、ここの知識はすでに持っているということを前提に話を進めさせていただきますので、ごめんなさい!
覚え方
では、さっそく簡単な覚え方を紹介していきます。
その前に、この表の見方を少し変えてもらう必要があります。
発想の転換が必要な覚え方ですので、頑張ってついてきてください。
まずは、JKフリップフロップの真理値表をもう一度見てください。下に再掲します。

この表の上の部分にJとKと書かれている部分がありますね、これが確認できたら、今度は下のほうを見てください。
0と1がそれぞれ書かれていると思います。ここからが少し「ん?」となる部分ですので、慎重に読んでいってください。
この、0と1を、それぞれアルファベットの O(オー) と I(アイ) という風に呼ぶようにしてください。
0をO(オー)、1をI(アイ)です。なんでそうなるんだよ、という疑問はとりあえず抑えてつけておきましょう。
ただの覚え方なので、気にしない気にしない。
そのうえで、上の部分のJとKをからませて、ローマ字を読むのと同じように読んでみます。
例えば、Jが0で、Kが1ならQの値は0となるので、
JOKIO(ジョキオ)
という風に読みます。下図↓
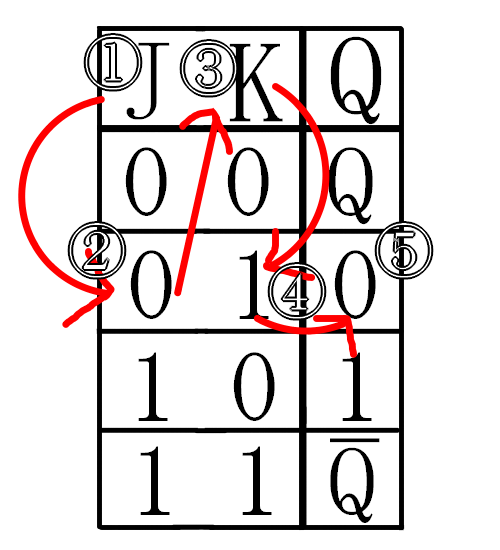
何となくお分かりいただけたでしょうか?
飲み込むまでに少し時間がかかるかもしれませんが、もし気になるところがあったとしても、これはあくまで覚え方ですので、こういうものなんだとおもってください。
上記の例のようにして読んでいくと、上から
JOKOQ(ジョコック)
JOKIO(ジョキオ)
JIKOI(ジコイ)
JIKI反転(ジキ反転)
<↑最後のこいつだけ少し変ですが、いったん流してください。>
というようになります。
この4つさえ覚えておけば、例えば
J→1,K→0
の組み合わせが出てきたとき、Jのところからローマ字読みのまま読んで・・・
「Jと1だから・・・ジ、Kと0だから・・・コ、ジとコ・・・ジコイだから1だ!」
という風に問題を解くことができます。
このやり方だと、単にそのまま覚えておくよりはるかに簡単に覚えられ、そして、早く思い出すことができます。
少し語呂合わせの覚え方に近いと思います。
少し解説
ちなみに、先ほどの”JOKIO”と”JIKOI”はわかったけど、”JOKOQ”と”JIKI反転”がいまいちわからんという人もいるかと思います。
これから説明するのでご安心を!
まず、JOKOQについてですが、前半のJOKOはよくわかると思います。
J→0,K→0のとき、という意味です。
そして、この時、Qのあたいは前回のQの値をそのまま持ち越すことになります。
つまり、前回のQが0なら次のQは0ですし、前回のQが1なら次のQも1となります。
このように、前の値によって結果が決まり、固定的ではないので、JOKOQという風に、出力の結果をQというようにあらわしているのです。
問題を解くときは、
J→0,K→0のとき、”JOKOQ”をすぐ思い出し、前回のQの値をみて、0なら0,1なら1と答えます。
次に、JIKI反転についてですが、JIKIはそのままのいみでOKです。
そして、
J→1、K→1
の時、その出力結果は、前回のQの値を反対にした値になります。
Qを使って表すのなら、”Qバー”になります。
ということはつまり、JIKIが来たら、Qを反転させるという風に覚えればいいわけです。
そういうわけで、”JIKI反転”となっています。
”JIKIQバー”でもよかったのかもしれませんが、語呂が何となく悪いと思ったので、JIKI反転にしました。
終わりに
今回の覚え方をマスターすれば、JKフリップフロップについていちいち復習しなくとも、ほぼ忘れることのないものとなります。
簡単に覚えられるものになっていますので、今ここで覚えてください!
この方法が役に立ったのなら幸いです!







